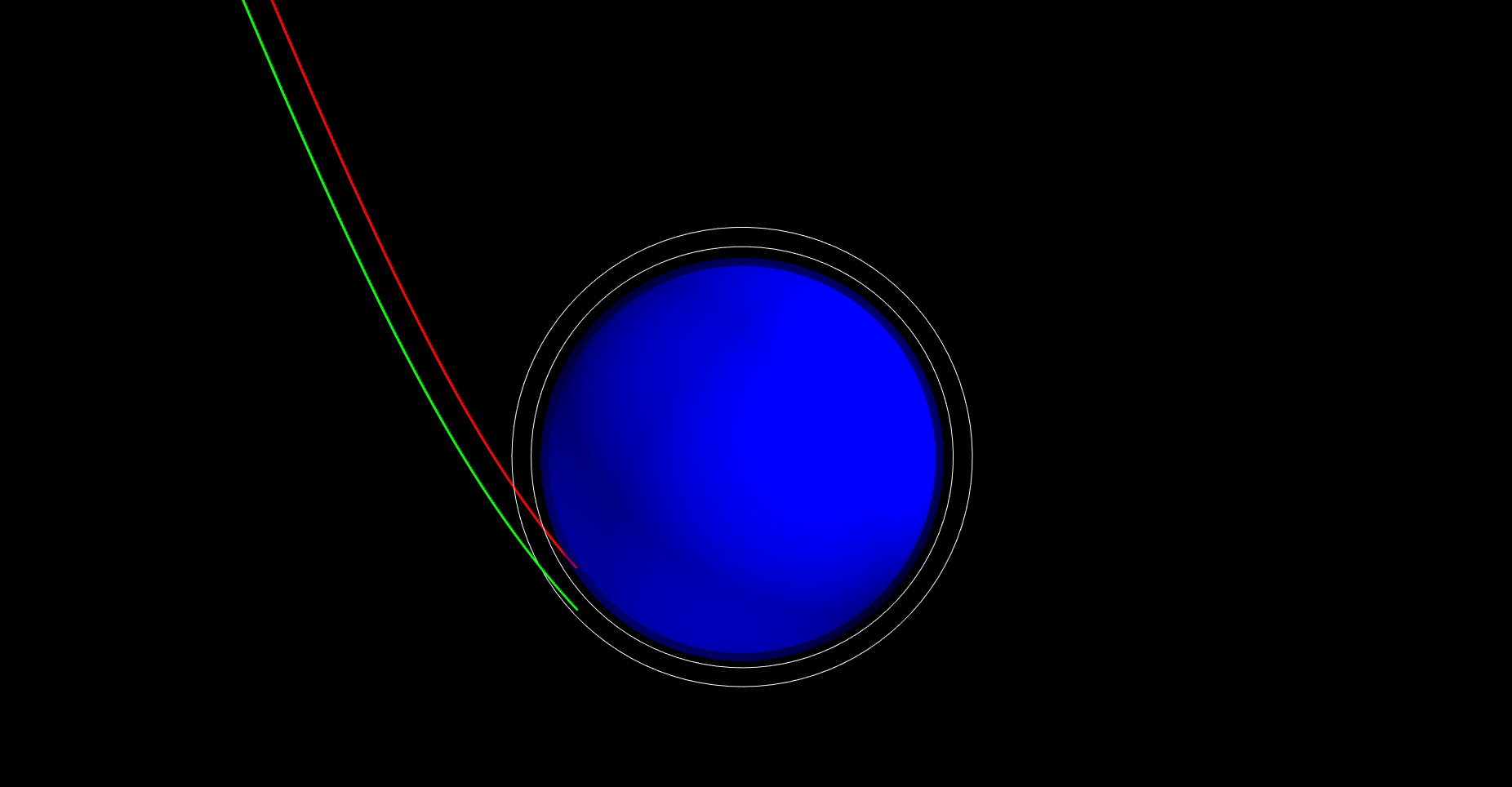
Example - 64 - Probe and Orbiter Trajectory

In this example, we illustrate the approach trajectories for an atmospheric entry probe, and an orbiter spacecraft which performs propulsive orbit insertion immediately after probe entry.

Note: This example requires Mayavi for visualization and requires the following packages to be to be installed in your virtual env: pyqt5, vtk, mayavi.

Note: For the 3D viz, tt is recommended that you run this example by running the python file using: python example-64-probe-and-orbiter-trajectory.py from your virtual env terminal instead of this Jupyter Notebook. If you use this Jupyter Notebook, then you need to have the following additional packages installed ipywidgets and ipyevents, and must do jupyter nbextension install --py mayavi --user before you start the notebook.

from mayavi import mlab
mlab.init_notebook(backend='ipy')

import numpy as np

from AMAT.approach import Approach

Notebook initialized with ipy backend.

Compute the approach trajectories for the probe and the orbiter spacecraft which performs orbit insertion at 4000 km periapsis altitude

probe = Approach("NEPTUNE",
                    v_inf_vec_icrf_kms=np.array([17.78952518, 8.62038536, 3.15801163]),
                    rp=(24764 + 400) * 1e3, psi=3*np.pi/2,
                    is_entrySystem=True, h_EI=1000e3)


space = Approach("NEPTUNE",
                    v_inf_vec_icrf_kms=np.array([17.78952518, 8.62038536, 3.15801163]),
                    rp=(24764 + 4000) * 1e3, psi=3*np.pi/2)

theta_star_arr_probe = np.linspace(-1.8, probe.theta_star_entry, 101)
pos_vec_bi_arr_probe = probe.pos_vec_bi(theta_star_arr_probe)/24764e3


theta_star_arr_space = np.linspace(-1.8, -0.03, 101)
pos_vec_bi_arr_space = space.pos_vec_bi(theta_star_arr_space)/24764e3

x_arr_probe = pos_vec_bi_arr_probe[0][:]
y_arr_probe = pos_vec_bi_arr_probe[1][:]
z_arr_probe = pos_vec_bi_arr_probe[2][:]

x_arr_space = pos_vec_bi_arr_space[0][:]
y_arr_space = pos_vec_bi_arr_space[1][:]
z_arr_space = pos_vec_bi_arr_space[2][:]


u = np.linspace(0, 2 * np.pi, 100)
v = np.linspace(0, np.pi, 100)
x = 1*np.outer(np.cos(u), np.sin(v))
y = 1*np.outer(np.sin(u), np.sin(v))
z = 1*np.outer(np.ones(np.size(u)), np.cos(v))

x1 = 1.040381198513972*np.outer(np.cos(u), np.sin(v))
y1 = 1.040381198513972*np.outer(np.sin(u), np.sin(v))
z1 = 1.040381198513972*np.outer(np.ones(np.size(u)), np.cos(v))


x_ring_1 = 1.1*np.cos(u)
y_ring_1 = 1.1*np.sin(u)
z_ring_1 = 0.0*np.cos(u)

x_ring_2 = 1.2*np.cos(u)
y_ring_2 = 1.2*np.sin(u)
z_ring_2 = 0.0*np.cos(u)

mlab.figure(bgcolor=(0,0,0))
s1 = mlab.mesh(x, y, z, color=(0,0,1))
s2 = mlab.mesh(x1, y1, z1, color=(0,0,1), opacity=0.3)
r1 = mlab.plot3d(x_ring_1, y_ring_1, z_ring_1, color=(1,1,1), line_width=1, tube_radius=None)
r2 = mlab.plot3d(x_ring_2, y_ring_2, z_ring_2, color=(1,1,1), line_width=1, tube_radius=None)

p1 = mlab.plot3d(x_arr_probe, y_arr_probe, z_arr_probe, color=(1,0,0), line_width=3, tube_radius=None)
p2 = mlab.plot3d(x_arr_space, y_arr_space, z_arr_space, color=(0,1,0), line_width=3, tube_radius=None)

mlab.show()

Plot the approach trajectories ofthe probe and the spacecraft orbiter

from IPython.display import Image
Image(filename="../plots/example-64-probe-and-orbiter-trajectory.png", width=800)

Compute the atmosphere-relative entry conditions for the probe

print("Entry altitude, km: "+ str(probe.h_EI/1e3))
print("Entry longitude BI, deg: "+ str(round(probe.longitude_entry_bi*180/np.pi, 2)))
print("Entry latitude BI, deg: "+ str(round(probe.latitude_entry_bi*180/np.pi, 2)))
print("Atm. relative entry speed, km/s: "+str(round(probe.v_entry_atm_mag/1e3, 4)))
print("Atm. relative heading angle, deg: "+str(round(probe.heading_entry_atm*180/np.pi, 4)))
print("Atm. relative EFPA, deg: "+str(round(probe.gamma_entry_atm*180/np.pi, 4)))

Entry altitude, km: 1000.0
Entry longitude BI, deg: -74.91
Entry latitude BI, deg: 1.66
Atm. relative entry speed, km/s: 27.866
Atm. relative heading angle, deg: 13.7856
Atm. relative EFPA, deg: -10.0695